BOJ 2664. 다각형의 확장

BOJ 2664. 다각형의 확장

2664번: 다각형의 확장

2년 전에 아주 고생하며 풀었던 문제인데, 당시 무슨 생각을 하면서 풀었는지 복기해보는 글입니다. 검은 배경의 그림은 2년 전 풀면서 직접 그렸던 그림입니다.

---

입력이 볼록 다각형인 경우를 생각해보면  아주 쉬워집니다. (가능한 볼록 다각형은 직사각형뿐이지만)

정확히는 볼록 다각형이 아니더라도, d-확장을 하는 과정에서 변들이 서로 만나서 '쌍소멸'할 가능성이 없는 경우도 똑같은 이유로 아주 쉽습니다. 이를 판별하는 방법은 도형에 안쪽으로 움푹 들어간 부분이 있는지를 확인해주면 됩니다.

 

좌: d-확장에서 변들이 쌍소멸하지 않는 예 / 우: 쌍소멸 가능성이 있는 예

그림을 보면 무슨 느낌인지 이해하기 쉬울 겁니다. 엄밀하게 구분을 해보자면, 서로 평행한 임의의 쌍의 변에 대해 공통수선이 존재할 때 임의의 공통수선이 다각형의 내부 또는 경계만을 지나는 경우가 지금 설명하려는 경우입니다. 물론 답을 코드로 구현할 때 이걸 구분할 필요는 없습니다. 이 문제에서 쉬운 케이스는 어려운 케이스의 부분집합에 불과합니다.

 

볼록 다각형, 즉 직사각형인 경우에서는 확장 후 도형의 형태를 생각해보면 결국 꼭짓점의 x좌표와 y좌표를 꼭짓점 기준으로 '바깥쪽'을 향해 적절히 증가/감소시켜주기만 하면 됩니다.

 

직사각형의 1-확장

직사각형이 아니더라도 앞서 얘기한 조건을 만족하는 다각형이라면 직사각형과 같은 방법으로 최종 도형을 구할 수 있습니다.

 

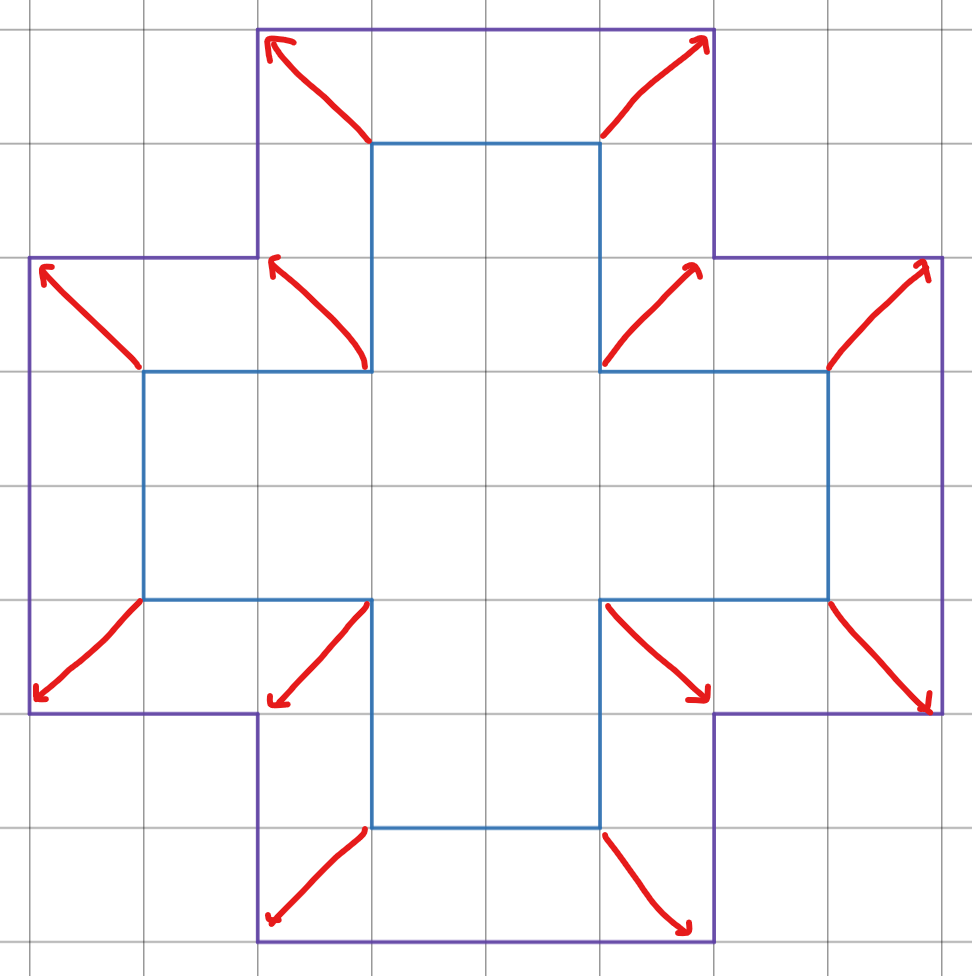
직사각형이 아닌 다각형을 1-확장한 예

'바깥쪽'이 어느 방향인지는, 입력의 좌표들이 반시계 방향으로 들어온다는 것을 생각하고, 이전 좌표, 현재 좌표, 다음 좌표의 x, y좌표의 증감을 따져보면 알 수 있습니다.

예를 들어 입력이 ..., (17, 5), (17, 13), (14, 13), ... 와 같다면, 현재 좌표 (17, 13)과 이전 좌표 (17, 5)는 y좌표가 +8만큼 차이 나고, 다음 좌표 (14, 13)과 현재 좌표 (17, 13)은 x좌표가 -3만큼 차이 납니다. 여기에 점들의 순서는 항상 반시계 방향이라는 정보를 조합하면 '바깥쪽'은 단 한 방향으로 결정됩니다. 이를 도식화하여 나타내면 아래 그림과 같습니다. 총 8가지 경우가 있고, 앞서 든 예시는 아래 그림의 2번 케이스에 해당됩니다. 아래 그림에서 각 상황을 나타내는 숫자는 코드의 구현에 그대로 사용되었습니다.

 

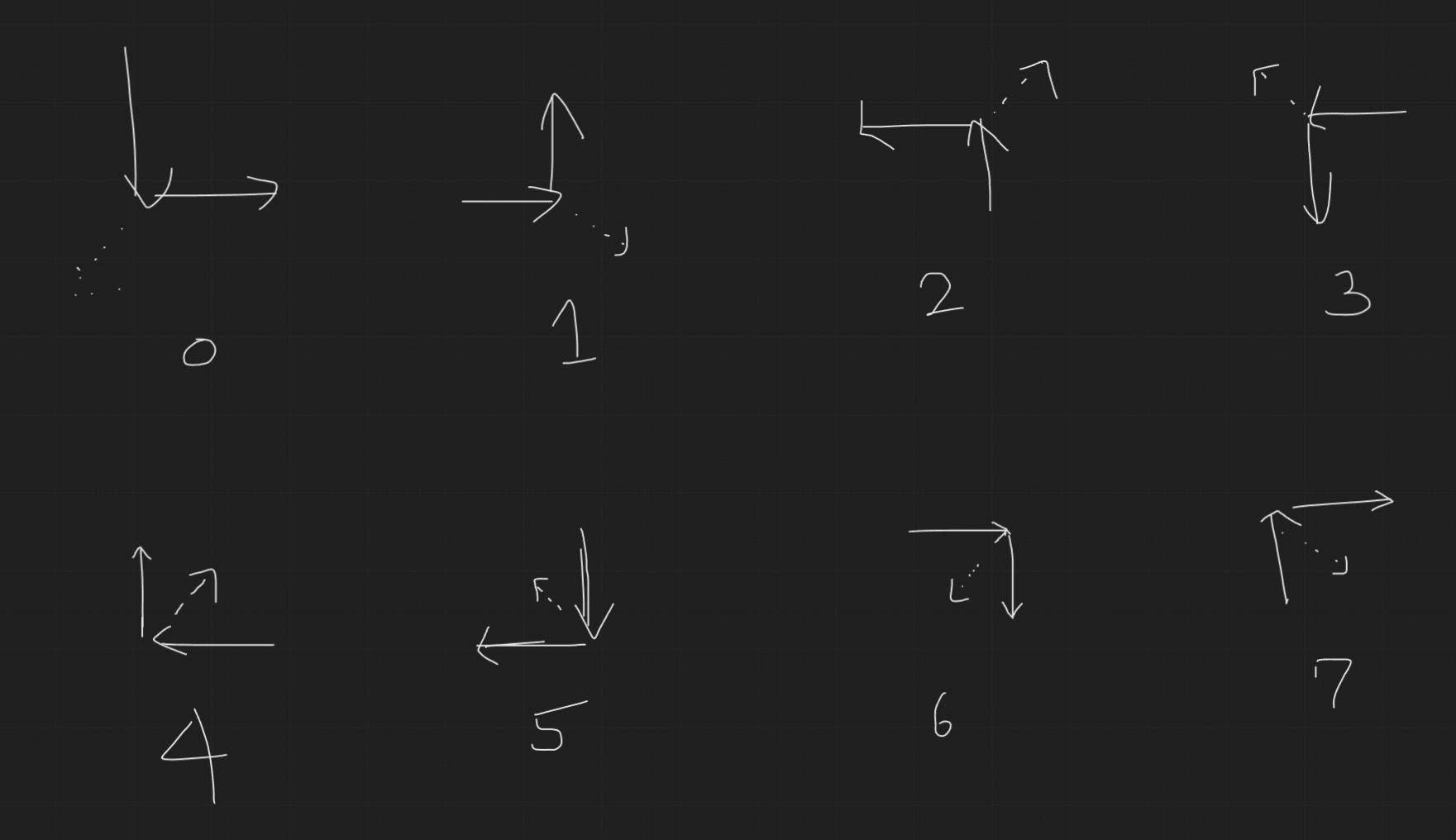
실선 화살표: 입력으로 주어진 점들의 진행 방향 / 점선 화살표: 실제 '바깥쪽'의 방향

쉬운 내용으로 지면을 많이 차지한 감이 없진 않지만 모두 완전한 풀이를 위한 기초적인 내용이 된다 생각하여 포함하였습니다. 변끼리 쌍소멸을 하는 경우에 대한 풀이도 위 방법을 기초로 하고, 쌍소멸에 대한 최소한의 직관이 있어야 앞으로 마주칠 무수한 반례들을 헤매지 않고 처리할 수 있습니다. 실제로 문제를 풀 때 어려운 예만 생각하다가 위 방법을 찾기까지도 시간이 상당히 걸려서 헤맸던 것으로 기억합니다.

 

이제 변들이 쌍소멸하는 경우를 생각해봅시다. 쌍소멸하지 않을 때는 바깥쪽 방향을 구해서 그 방향으로 좌표를 수정해줬는데, 이번에도 그 방법이 먹히는지 한 번 해보면 아래 그림과 같은 결과를 얻을 수 있습니다.

 

흰색 점들이 확장 후 다각형의 꼭짓점, 나머지는 소멸

그림의 점선을 보니 당시에는 각 꼭짓점을 중심으로 하는 2d*2d 정사각형을 그리고 겹치는 부분을 구하자는 생각을 잠시 한 것 같은데, 딱히 도움이 되는 아이디어 같지는 않습니다.

 

각 꼭짓점을 바깥쪽으로 이동시킨 점들을 순서대로 이은 모습

이 그림처럼 꼭짓점을 앞서 설명한 방법대로 이동시키고, 그들을 순서대로 이은 뒤 처리하는 것이 큰 효과를 볼 수 있었습니다. 위의 그림을 통해, 예시에서는 중간에 교차점이 하나 생기고, 3개의 점이 삭제되어야 한다는 것을 알 수 있습니다.

꼭짓점들을 확장하고 이었을 때 교차하는 두 선분이 있다면, 그 두 선분 사이의 선분은 모두 무시한 뒤 교차점을 추가해주면 된다는 생각을 한 것 같습니다.

 

일직선상에서 교차할 수도 있다!

첫 코드를 짜기 전에 찾아낸 예시인데, 예상과는 다르게 일직선상에서 교차하는 경우도 가능해서 고려를 해주어야 합니다. 이 경우에서는 교차점을 추가할 것이 아니라, 시작 선분의 시작점과 끝 선분의 끝점 사이의 모든 점을 지우면 됩니다.

 

일단 위 아이디어만을 구현한 코드입니다. determine은 각 점에서 '바깥쪽'을 판별하는 함수이고, cross는 주어진 선분에 대해 가장 마지막으로 교차하는 선분을 구하고 상황에 맞게 점을 삭제/추가하는 함수입니다.

 

코드

#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int, int> pi;

int d, n, ans = 0;
vector<pi> po(51, {-1, -1}), ext(51, {-1, -1});
vector<int> sh(51);
queue<int> coord;

pi operator +(const pi& p, const pi& d){
    return make_pair(p.x + d.x, p.y + d.y);
}

int determine(int i)
{
    if(i == 0) return 0;
    if(po[i - 1].x == po[i].x){
        if(po[i - 1].y > po[i].y){
            if(po[i].x < po[i + 1].x)
                return 0;
            return 5;
        }
        if(po[i].x < po[i + 1].x)
            return 7;
        return 2;
    }
    if(po[i - 1].x > po[i].x){
        if(po[i].y < po[i + 1].y)
            return 4;
        return 3;
    }
    if(po[i].y < po[i + 1].y)
        return 1;
    return 6;
}

int cross(int p)
{
    int xp1 = ext[p].x, xp2 = ext[p + 1].x, yp1 = ext[p].y, yp2 = ext[p + 1].y;
    int ret = -1;
    if(p == n - 1) return ret;
    bool vert = (yp1 == yp2);
    for(int i = p + 2; i < n; i++){
        if(p == 0 && i == n - 1) break;
        if(ext[i].y == ext[i + 1].y){
            // 가로 가로
            if(vert){
                if(yp1 == ext[i].y && min(xp1, xp2) < ext[i].x && ext[i].x < max(xp1, xp2) && (ext[i + 1].x > max(xp1, xp2) || ext[i + 1].x < min(xp1, xp2))){
                    ret = i;
                    ext[p + 1] = make_pair(-1, -1);
                }
            }
            // 세로 가로
            else if((min(yp1, yp2) <= ext[i].y && ext[i].y <= max(yp1, yp2)) && min(ext[i].x, ext[i + 1].x) <= xp1 && xp1 <= max(ext[i].x, ext[i + 1].x)){
                ret = i;
                ext[p + 1] = make_pair(xp1, ext[i].y);
            }
        }
        else{
            // 가로 세로
            if(vert){
                if((min(ext[i].y, ext[i + 1].y) <= yp1 && yp1 <= max(ext[i].y, ext[i + 1].y)) && min(xp1, xp2) <= ext[i].x && ext[i].x <= max(xp1, xp2)){
                    ret = i;
                    ext[p + 1] = make_pair(ext[i].x, yp1);
                }
            }
            // 세로 세로
            else if(xp1 == ext[i].x && min(yp1, yp2) < ext[i].y && ext[i].y < max(yp1, yp2) && (ext[i + 1].y > max(yp1, yp2) || ext[i + 1].y < min(yp1, yp2))){
                ret = i;
                ext[p + 1] = make_pair(-1, -1);
            }
        }
    }
    return ret;
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> d >> n;
    for(int i = 0; i < n; i++)
        cin >> po[i].x >> po[i].y;
    po[n] = {po[0].x, po[0].y};
    for(int i = 0; i <= n; i++){
        sh[i] = determine(i);
        if(sh[i] == 0 || sh[i] == 6){
            ext[i] = po[i] + make_pair(-d, -d);
        }
        else if(sh[i] == 1 || sh[i] == 7){
            ext[i] = po[i] + make_pair(d, -d);
        }
        else if(sh[i] == 2 || sh[i] == 4){
            ext[i] = po[i] + make_pair(d, d);
        }
        else{
            ext[i] = po[i] + make_pair(-d, d);
        }
    }
//    for(int i=0;i<n;i++) cout << i << ": " << ext[i].x << ' ' << ext[i].y << '\n';
//    cout << "\n\n";
    for(int i = 0; i < n; i++){
        int check = cross(i);
//        cout << "After " << i << ": " << check << '\n';
//        for(int k=0;k<n;k++) cout << k << ": " << ext[k].x << ' ' << ext[k].y << '\n';
        if(check == -1) continue;
        for(int j = i + 2; j <= check; j++)
            ext[j] = make_pair(-1, -1);
        i = check;
//        cout << "Now " << i << ": " << check << '\n';
//        for(int k=0;k<n;k++) cout << k << ": " << ext[k].x << ' ' << ext[k].y << '\n';
    }
//    for(int i=0;i<n;i++) cout << i << ": " << ext[i].x << ' ' << ext[i].y << '\n';
    for(int i = 0; i < n; i++){
        if(ext[i] != make_pair(-1, -1)){
            ans++;
            coord.push(i);
        }
    }
    cout << ans << '\n';
    while(!coord.empty()){
        cout << ext[coord.front()].x << ' ' << ext[coord.front()].y << '\n';
        coord.pop();
    }
    return 0;
}

 

한 점에서만 만나면서 교차하는 경우

위 코드는 일직선상 교차를 처리할 때 부등호를 잘못 넣어 위와 같이 한 점에서 만나는 경우에 저 한 점을 삭제하지 못하는 문제가 있습니다.

 

왜 안되는지 한참 고민한 반례

위 예시에 대한 출력으로 원래는 직사각형이 나와야 하는데 직사각형이 나온 뒤 좌상단 교차점이 두 번 더 찍혀 나옵니다. 이는 사실 determine 함수에서 i가 n일 때에 대한 처리를 안 해주어 생긴 오류였습니다.

 

이상한 실수를 두세 번 하고 다 고쳤다고 느낄 때쯤...

 

확장 과정에서 내부가 다 채워지고 답은 직사각형이 나오는 예시입니다. 답은 당연히 네 꼭짓점인데, 네 꼭짓점 이외에도 그림에서 왼쪽 변의 (4, 44)라고 표시된 점이 두 번 추가로 나옵니다. 이건 사실 구현 방식 자체가 틀렸다는 걸 알 수 있는 예시인데, 좌상단의 (4, 106)에서 교차하는 변 제거를 시작하면 (4, 44)에서 끝나는 선분은 시작 선분과 합쳐져서 그 선분 자체는 내부적으로 없어지게 됩니다. 그 없어진 선분으로부터 다시 제거를 해야 하는데, 그렇지 못했기 때문에 (4, 44)가 제대로 지워지지 않은 것입니다. 이를 해결하기 위해서는 선분을 지우기 전에 지우려는 선분이 이후 교차에 관여하는지를 먼저 확인해주어야 합니다. 그리고 이는 다행히도 재귀를 사용하면 간단하게 변경할 수 있는 부분입니다.

 

최종 정답을 받은 코드입니다. cross 함수를 보면, 한 선분이 다른 선분과 교차하는 경우 재귀적으로 교차를 탐색하는 것을 알 수 있습니다.

 

코드

#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int, int> pi;

int d, n, ans = 0;
vector<pi> po(51, make_pair(-1, -1)), ext(51, make_pair(-1, -1));
vector<int> sh(51);
queue<int> coord;

pi operator +(const pi& p, const pi& d){
    return make_pair(p.x + d.x, p.y + d.y);
}

int determine(int i)
{
    if(i == 0 || i == n) return 0;
    if(po[i - 1].x == po[i].x){
        if(po[i - 1].y > po[i].y){
            if(po[i].x < po[i + 1].x)
                return 0;
            return 5;
        }
        if(po[i].x < po[i + 1].x)
            return 7;
        return 2;
    }
    if(po[i - 1].x > po[i].x){
        if(po[i].y < po[i + 1].y)
            return 4;
        return 3;
    }
    if(po[i].y < po[i + 1].y)
        return 1;
    return 6;
}

int cross(int p)
{
    int xp1 = ext[p].x, xp2 = ext[p + 1].x, yp1 = ext[p].y, yp2 = ext[p + 1].y;
    int ret = -1;
    if(p == n - 1) return ret;
    bool vert = (yp1 == yp2);
    for(int i = p + 2; i < n; i++){
        int xi1 = ext[i].x, xi2 = ext[i + 1].x, yi1 = ext[i].y, yi2 = ext[i + 1].y;
        if(p == 0 && i == n - 1) break;
        if(yi1 == yi2){
            // 가로 가로
            if(vert){
                if(yp1 == yi1 && min(xp1, xp2) <= xi1 && xi1 <= max(xp1, xp2) && (xi2 >= max(xp1, xp2) || xi2 <= min(xp1, xp2))){
                    ret = i;
                    ext[p + 1] = make_pair(-1, -1);
                }
            }
            // 세로 가로
            else if((min(yp1, yp2) <= yi1 && yi1 <= max(yp1, yp2)) && min(xi1, xi2) <= xp1 && xp1 <= max(xi1, xi2)){
                ret = i;
                ext[p + 1] = make_pair(xp1, yi1);
            }
        }
        else{
            // 가로 세로
            if(vert){
                if((min(yi1, yi2) <= yp1 && yp1 <= max(yi1, yi2)) && min(xp1, xp2) <= xi1 && xi1 <= max(xp1, xp2)){
                    ret = i;
                    ext[p + 1] = make_pair(xi1, yp1);
                }
            }
            // 세로 세로
            else if(xp1 == xi1 && min(yp1, yp2) <= yi1 && yi1 <= max(yp1, yp2) && (yi2 >= max(yp1, yp2) || yi2 <= min(yp1, yp2))){
                ret = i;
                ext[p + 1] = make_pair(-1, -1);
            }
        }
    }
    if(ret != -1) cross(ret);
    for(int j = p + 2; j <= ret; j++){
        ext[j] = make_pair(-1, -1);
    }
    return ret;
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> d >> n;
    for(int i = 0; i < n; i++)
        cin >> po[i].x >> po[i].y;
    po[n] = {po[0].x, po[0].y};
    for(int i = 0; i <= n; i++){
        sh[i] = determine(i);
        if(sh[i] == 0 || sh[i] == 6){
            ext[i] = po[i] + make_pair(-d, -d);
        }
        else if(sh[i] == 1 || sh[i] == 7){
            ext[i] = po[i] + make_pair(d, -d);
        }
        else if(sh[i] == 2 || sh[i] == 4){
            ext[i] = po[i] + make_pair(d, d);
        }
        else{
            ext[i] = po[i] + make_pair(-d, d);
        }
    }
//    for(int i=0;i<=n;i++) cout << i << ": " << ext[i].x << ' ' << ext[i].y << '\n';
//    cout << "\n\n";
    for(int i = 0; i < n; i++){
        int check = -1;
        if(ext[i] != make_pair(-1, -1))
            check = cross(i);
        if(check != -1) i = check;
//        cout << "After " << i << ": " << check << '\n';
//        for(int k=0;k<n;k++) cout << k << ": " << ext[k].x << ' ' << ext[k].y << '\n';
//        if(check == -1) continue;
//        for(int j = i + 2; j <= check; j++)
//            ext[j] = make_pair(-1, -1);
//        i = check;
//        cout << "Now " << i << ": " << check << '\n';
//        for(int k=0;k<n;k++) cout << k << ": " << ext[k].x << ' ' << ext[k].y << '\n';
    }
//    for(int i=0;i<n;i++) cout << i << ": " << ext[i].x << ' ' << ext[i].y << '\n';
    for(int i = 0; i < n; i++){
        if(ext[i] != make_pair(-1, -1)){
            ans++;
            coord.push(i);
        }
    }
    cout << ans << '\n';
    while(!coord.empty()){
        cout << ext[coord.front()].x << ' ' << ext[coord.front()].y << '\n';
        coord.pop();
    }
    return 0;
}