BOJ 5470. 균형잡힌 직선형 정원 (DP X 풀이)

https://www.acmicpc.net/problem/5470

5470번: 균형잡힌 직선형 정원

DP로 쉽게? 플2가 쉬운지는 모르겠지만 하여튼 풀린다고 하는데 DP를 못해서 다르게 풀어봤습니다.

 

---

무언가가 오름차순으로 몇 번째에 있는지를 구할 때 자주 쓰는 방법이, 앞자리부터 보면서 자리별로 '건너뛴' 경우의 수를 세서 더하는 것입니다. 'ability'라는 단어가 사전에서 몇 번째에 있는지를 알고 싶다면, 먼저 aa로 시작하는 모든 단어의 수를 더하고, ab로 시작하는 단어 중에서도 aba로 시작하는 단어, abb로 시작하는 단어, ..., abh로 시작하는 단어들의 수를 전부 더하고, 이 과정을 ability가 나올 때까지 하는 것이죠.

 

이 문제에서는 문자열의 자릿수는 정해져 있기 때문에 앞의 몇 자리가 이미 채워져 있는 문자열에 대해서 뒤의 빈 자리를 채울 수 있는 경우의 수를 구하면 됩니다.

 

LPPLP라는 문자열을 예로 들면, L만 보았을 때는 아직 오름차순으로 가장 앞이기 때문에 아무것도 더하지 않고, LP까지 보았을 때는 오름차순으로 더 앞에 있는 LLXXX를 전부 건너뛰었으므로 LLXXX의 개수를 구해서 더해주어야 합니다. LPP까지 본다면, LPLXX를 전부 건너뛰었으므로 LPLXX의 개수를 구해서 또 더해주어야 합니다. 이 과정을 마지막 문자까지 반복하면 해당 문자열이 오름차순으로 몇 번째인지 알아낼 수 있습니다.

 

이제 앞서 말했던 것처럼 문자열의 일부가 주어졌을 때 나머지를 채우는 경우의 수를 구하는 법을 알아내면 됩니다.

---

문자열에는 L 또는 P가 올 수 있는데, 여기서 L을 +1, P를 -1이라고 해봅시다. 이제 f(k)를 문자열의 0~k번째 문자의 값의 합으로 정의합시다. 예를 들어, 문자열이 LPPLP라면 f(1)=1, f(2)=0, f(3)=-1, f(4)=0, f(5)=-1입니다.

f와 문제의 조건 사이의 관계를 생각해보면, 가장 간단하게는 f의 절댓값은 2를 넘을 수 없습니다. |f(k)|가 2를 넘는 k가 존재한다면 [1, k] 구간에서 L과 P의 개수 차이가 2를 넘기 때문입니다.

 

f의 그래프를 몇 번 그려보고 조금 더 생각해보면, 가장 타이트한 조건은 f의 최솟값과 최댓값의 차이가 2 이하이어야 한다는 것입니다. 최솟값과 최댓값이 시작과 끝인 구간을 잡으면, L과 P의 개수의 차이가 곧 f의 최솟값과 최댓값의 차이이기 때문입니다. 그리고 이 구간보다 L과 P의 개수 차이가 큰 구간은 없습니다.

 

따라서 조건을 만족하려면, f(0)=0이므로 한 문자열에 대해 f의 치역이 [-2, 0], [-1, 1], [0, 2] 중 하나가 되어야 합니다. 아래 그림에 각 경우에 대한 예시가 있는데, 어떠한 경우에도 이 셋 중 적어도 하나에 해당됩니다.

 

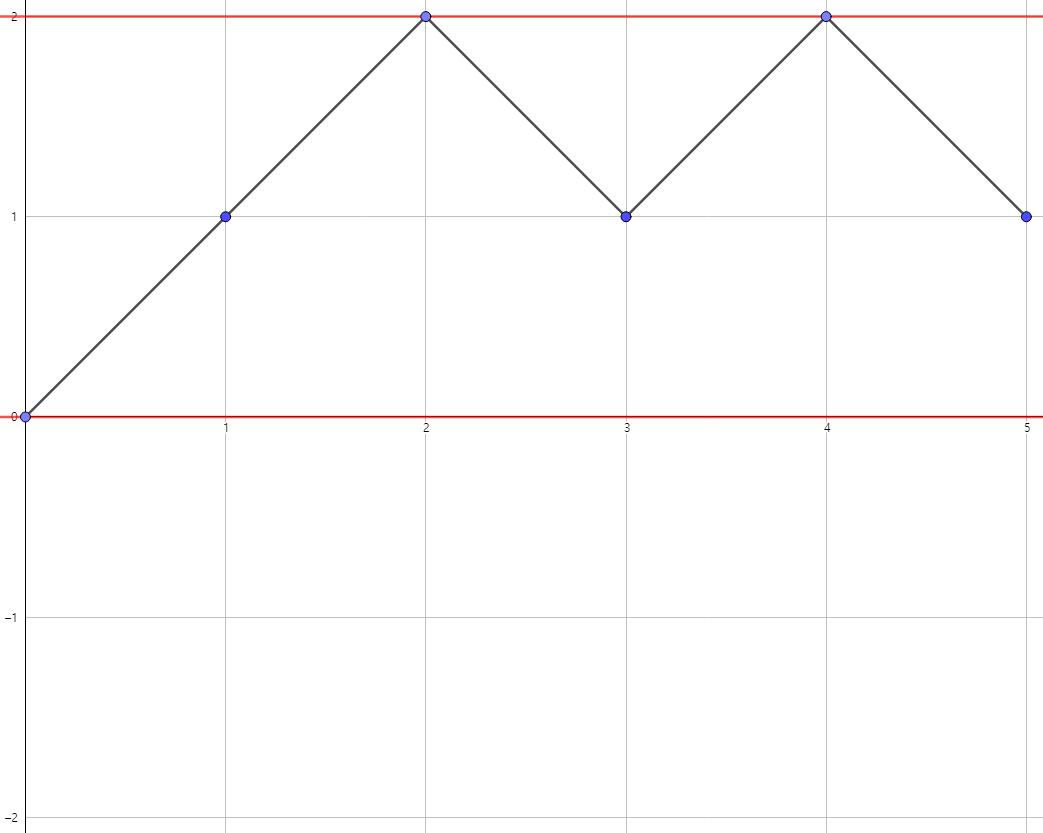
LLPLP에 대한 f의 그래프, 치역은 [0, 2]

LPPLP에 대한 f의 그래프, 치역은 [-1, 1]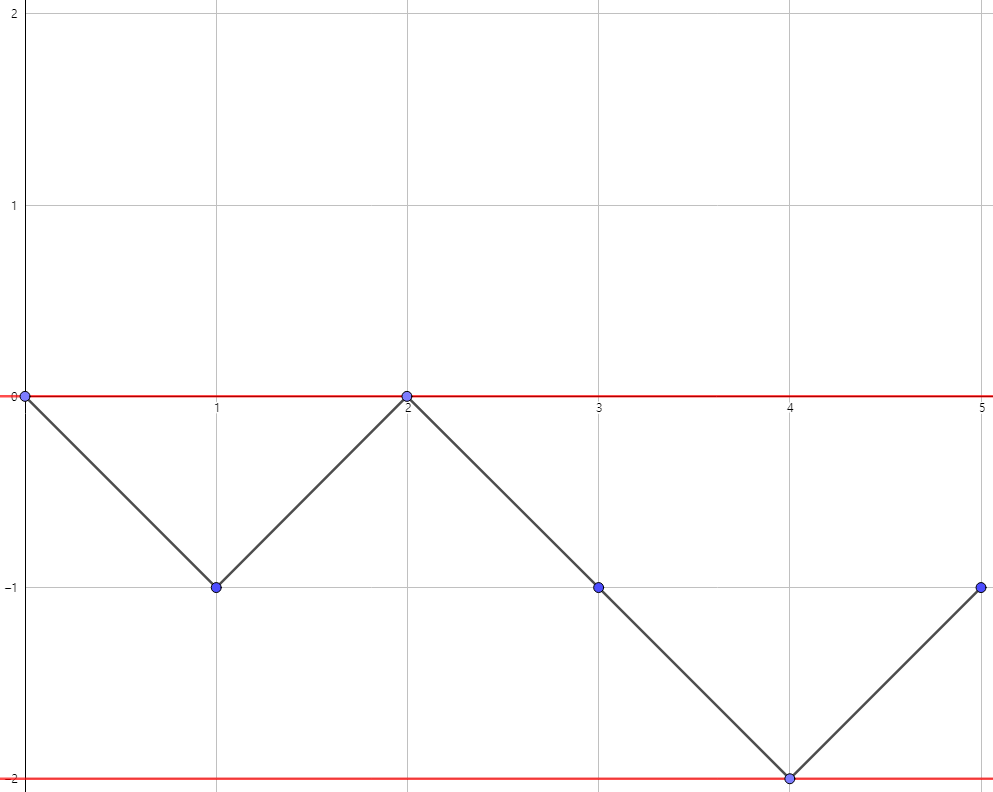

PLPPL에 대한 f의 그래프, 치역은 [-2, 0]

경우의 수를 본격적으로 구해봅시다. 일반성을 잃지 않고 f의 치역이 [0, 2]라고 가정하면, f의 값이 0일 때는 반드시 다음 문자로 L이 오고, 2일 때는 반드시 다음 문자로 P가 옵니다. 이렇게 되면, 선택지가 있는 경우는 f의 값이 1인 경우뿐이라는 것을 알 수 있습니다. f(0)은 0으로 고정되어 있으니 f(1)은 자동적으로 1이 되고, f(2)는 0 또는 2가 되고, f(3)은 다시 무조건 1이 되고, ... 하는 과정이 반복됩니다. 짝수 번째 문자로 넘어갈 때만 f의 값에 대한 선택지(2가지)가 생기고, 홀수 번째 문자에서는 선택지가 하나로 고정되는 것입니다. 짝수 번째 문자에서의 선택지는 서로 독립적이므로, 만약 주어진 상태에서 f의 값이 1이고 앞으로 n자리를 더 채워야 한다면 경우의 수는 $ 2^{\frac{n+1}{2}} $이 됩니다. 기존 상태에서 f의 값이 0 또는 2였다면 경우의 수는 $ 2^{\frac{n}{2}} $이 되겠죠.

 

이미 주어진 문자열에서 너비가 2인 치역이 확정이 되는 경우에는 그저 위 식을 이용해서 세주면 됩니다. 마지막으로 생각해야 할 경우는 주어진 문자열에서 치역이 확정되지 않는 경우입니다. 다행히도 서로 대칭적인 두 가지 경우밖에 없습니다.

 

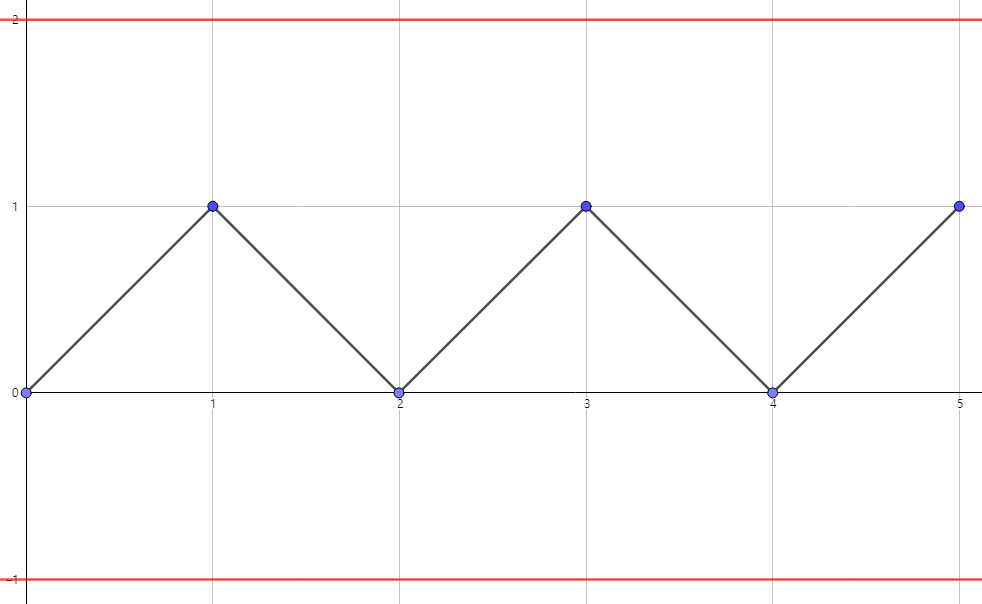
LPLPL에 대한 f의 그래프, [-1, 2]에서 확정되지 않은 치역

위처럼 치역이 확정되지 않는 경우 경우의 수를 전부 세고자 한다면, 치역이 [0, 2]가 되는 경우와 [-1, 1]이 되는 경우를 전부 고려해야 합니다. 치역이 정해진 상태에서 경우의 수를 세면 앞서 구한 경우와 다를 바 없지만, 끝까지 문자열을 채워도 LPLPLPL...이 반복되어 치역이 정해지지 않는 경우가 단 하나 있다는 차이점이 있습니다. 따라서 이 경우는 $ 2^{\frac{n}{2}} + 2^{\frac{n+1}{2}} - 1 $이 경우의 수가 됩니다.

 

실제 구현은 문자열 한 글자마다 '건너뛸' 경우의 수가 있는지 체크하여 더하는 방식입니다. f값을 쭉 기록하고, 각 시점에서 f의 최솟값과 최댓값을 기록하여 치역을 관리하였습니다.

 

코드

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef pair<int, int> pi;
typedef pair<int, pi> pii;
typedef pair<ll, ll> pl;
typedef pair<ll, pl> pll;
#define fi first
#define se second
#define pb push_back

const int MAX = 1e6;
ll N, M, h = 0, l = 0, c = 0, ans = 1;
string s;

ll power(ll a, ll b, ll mod = M)
{
    if(a == 0) return 0;
    if(a == 1) return 1;
    if(b == 0) return 1;
    if(b == 1) return a % mod;
    ll ret = 1;
    while(b){
        if(b % 2) ret = (ret * a) % mod;
        a = (a * a) % mod;
        b /= 2;
    }
    return ret;
}

ll f(int h, int l, int c, int k)
{
    if(h - l > 2) return 0;
    if(h - l == 2){
        if(c == h-1) return power(2, (k+1)/2);
        else return power(2, k/2);
    }
    return (power(2, (k+1)/2) + power(2, k/2) - 1) % M;
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> N >> M >> s;
    for(int i = 0; i < N; i++){
        if(s[i] == 'L'){
            ++c;
            h = max(h, c);
        }
        else{
            ans = (ans + f(max(h, c+1), l, c+1, N-i-1)) % M;
            --c;
            l = min(l, c);
        }
    }
    cout << ans << '\n';
    return 0;
}